8. Пример выполнения расчетной части проекта
8.1. Оптимизации запасов ресурсов
в традиционной постановке
Одной из важнейших задач логистики является задача оптимизации величины запасов ресурсов, необходимых для реализации производственной программы. Излишние запасы ресурсов приводят к увеличению потерь предприятия, связанных с хранением этих излишков, и потерь вследствие иммобилизации финансовых средств. Дефицит ресурсов приводит к недовыпуску продукции и к связанным с этим потерям (потери прибыли, штрафы посредникам и пр.).
Задача оптимизации производственной программы предприятия в простейшем случае имеет вид:
Например, пересчет элемента первого столбца первой строки:
где cij – нормы расхода j-того вида ресурсов на производство единицы i-того вида продукции;
Cj – запасы ресурсов j-того вида;
n – количество видов продукции;
m – количество видов ресурсов;
F – целевая функция (прибыль);
pi – прибыль от реализации единицы i-того вида продукции.
Под ресурсами здесь следует понимать сырье, материалы, оборудование, трудовые ресурсы и пр.
Решение этой задачи позволяет при имеющихся запасах ресурсов определить оптимальное количественное соотношение выпускаемых изделий, но никак не учитывает потерь, связанных с хранением излишних запасов и с иммобилизацией денежных средств, связанных с этими ресурсами.
Пример решения задачи традиционным способом
Составим математическую модель задачи. В качестве элементов решения задачи примем Х1 – число коров, Х2 – число десятков куриц.
На содержание одной коровы в год расходуется 2,1 т силоса, запас которого составляет 1050 т. Таким образом получаем первое ограничение:
по силосу 2,1Х1 ≤ 1050.
Аналогично получаем ограничения и по другим ресурсам:
| по комбикорму |
|
Х1 + 0,54Х2 ≤ 600; |
| по зерну |
|
0,6Х2 ≤ 20; |
| по выпасу |
|
Х1 ≤ 500; |
| по трудовым ресурсам |
|
10,5Х1 + 2,5Х2 ≤ 7300. |
Естественные или тривиальные ограничения:
Х1 ≥ 0; Х2 ≥ 0.
Прибыль, получаемая от реализации одной коровы, составляет 40 у.е., а от десятка куриц – 1 у.е. за десяток. В результате прибыль, получаемая от всей продукции, определяется выражением:
F= 40Х1+1Х2 → max.
Тогда математическая модель будет иметь вид:
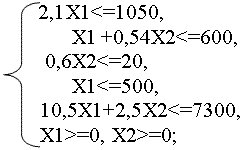
F=40Х1+1Х2 → max
Приведем задачу к канонической форме путем введения дополнительных переменных:
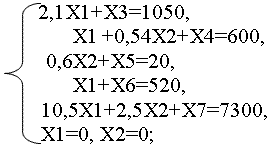
F – 40Х1 – 1Х2 = 0.
Это задача линейного программирования с двумя переменными. Она может быть решена графическим и симплекс-методом [
1,
2
].
При решении задачи графическим методом переходим от неравенств к равенствам:
2,1Х1 = 1050;
Х1 + 0,54Х2 = 600;
0,6Х2 = 20;
Х1 = 500;
10,5Х1 + 2,5Х2 = 7300.
Это уравнения прямых линий, которые могут быть легко построены по двум точкам.
Первое ограничение – вертикальная прямая линия при
Х1=1050/2,1=500.
Второе ограничение строим по двум точкам:
Х1=0; Х2=600/0,54=1111.
X2=0; X1=600/1=600.
Третье ограничение – горизонтальная линия при
Х2=20/0,6=33,3.
Четвертое ограничение – вертикальная прямая при
Х1=500.
Пятое ограничение – линия, которая строится по двум точкам:
Х1=0; Х2=7300/2,5=2920.
Х2=0; Х1=7300/10,5=695.
Тривиальные ограничения располагаются по осям.
Каждое ограничение неравенство отсекает полуплоскость. Система ограничений неравенств, если они совместны (не противоречат друг другу), образуют многоугольник допустимых решений. Оптимальное решение достигается в одной из вершин этого многоугольника. Для определения этой вершины необходимо построить линию уровня и перемещать ее в направлении градиента до крайней точки области допустимых решений.
Целевая функция может быть также построена по двум точкам. Придадим значение F=0:
F=40Х1+1Х2=0.
Это также уравнение прямой линии.
Х1=0; Х2=0.
Х1=1; Х2 = –40/1 = –40.
Градиент целевой функции перпендикулярен линии уровня, и его координаты определяются частными производными по каждой переменной:
GradF={dF/dX1;dF/dX2}={40,1}.
Результаты решения графическим методом приведены на рис. 8.1.
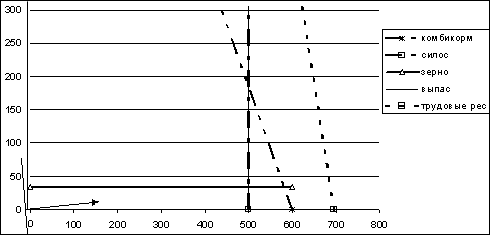
Рис. 8.1. Графическое решение задачи (первая итерация)
Графический метод более нагляден, а симплекс-метод более точен и позволяет количественно определить остатки ресурсов.
Приведем задачу к канонической форме путем введения дополнительных переменных:
| Силос |
|
2,1Х1 + Х3 = 1050; |
| Комбикорм |
|
Х1+ 0,54Х2 +Х4 = 600; |
| Зерно |
|
0,6Х2 + Х5 = 20; |
| Выпас |
|
Х1 + Х6 = 500; |
| Трудовые ресурсы |
|
10,5Х1 + 2,5Х2 +Х7 = 7300; |
| Прибыль |
|
F – 40Х1 – 1Х2 = 0. |
Дополнительные переменные определяются разностью между правой и левой частями ограничений-неравенств, те. разностью между запасами и использованием соответствующих ресурсов. Иначе говоря, они характеризуют остатки ресурсов.
Решение задачи симплексным методом приведено в табл. 8.2.
Решение задачи на этом этапе в краткой форме записи имеет вид:
X=(500; 33,3; 0; 82; 0; 0; 1966,66); F=20033.
Здесь значения переменных записаны в порядке возрастания их индексов, т е.
Х1=500; Х2=33,3; Х3=0; Х4=82; Х5=Х6=0; Х7=1966,6. F=20033.
Таблица 8.2
Решение задачи симплексным методом (первая итерация)
| Базис |
Х1 | Х2 | Х3 | Х4 |
Х5 | Х6 | Х7 |
Aio |
Aio/Air |
| Х3 |
2,1 |
0 |
1 |
0 |
0 |
0 |
0 |
1050 |
500 |
| Х4 |
1 |
0,54 |
0 |
1 |
0 |
0 |
0 |
600 |
600 |
| Х5 |
0 |
0,6 |
0 |
0 |
1 |
0 |
0 |
20 |
∞ |
| Х6 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
500 |
500 |
| Х7 | 10,5 | 2,5 | 0 | 0 |
0 | 0 | 1 | 7300 | 695,2 |
| F | –40 | –1 | 0 | 0 | 0 | 0 | 0 | 0 | |
| Х3 |
0 |
0 |
1 |
0 |
0 |
–2,1 |
0 |
0 |
∞ |
| Х4 |
0 |
0,54 |
0 |
1 |
0 |
–1 |
0 |
100 |
185,2 |
| Х5 |
0 |
0,6 |
0 |
0 |
1 |
0 |
0 |
20 |
33,33 |
| Х1 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
500 |
∞ |
| Х7 | 0 | 2,5 | 0 | 0 |
0 | –10,5 | 1 | 2050 | 820 |
| F | 0 | –1 | 0 | 0 | 0 | 40 | 0 | 20000 | |
| Х3 |
0 |
0 |
1 |
0 |
0 |
–2,1 |
0 |
0 |
|
| Х4 |
0 |
0 |
0 |
1 |
–0,83 |
–1 |
0 |
82 |
|
| Х2 |
0 |
1 |
0 |
0 |
1,666 |
0 |
0 |
33,33 |
|
| Х1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
500 |
|
| Х7 | 0 | 0 | 0 | 0 |
–4,17 | –10,5 | 1 | 1966,6 | |
| F | 0 | 0 | 0 | 0 | 1,66 | 40 | 0 | 20033 | |
Это означает, что при имеющихся запасах ресурсов максимальная прибыль, в размере 20033 у.е., может быть получена при производстве 500 коров и 33 десятков куриц. При этом остается излишек таких ресурсов, как комбикорм (Х4=82 т) и трудовые ресурсы (Х7=1966,6 чел.-дней).
Проверка:
2,1×500+0=1050;
1×500+0,54×33,3+82=600;
0+0,6×33,33+0= 20;
500+0+0= 500;
10,5×500+2,5×33,3+1966,6=7300;
F=40×500+1×33,3=20033.
Определим деньги, вложенные в ресурсы:
1050×25+600×64+20×60+500×70+7300×3,18=124064 у.е.
Для уменьшения затрат, связанных с хранением запасов, их излишки следует продать или сдать в аренду. Это позволит направить освободившиеся денежные средства на закупку дефицитных ресурсов с целью увеличения выпуска продукции. Однако полностью излишки продавать нецелесообразно, так как в этом случае эти ресурсы в свою очередь окажутся в дефиците, что не позволит увеличить объем выпуска продукции. Закупленные же ресурсы окажутся в избытке.
Увольняя часть рабочих, высвобождаем 1000 чел.-дней. Один человеко-день стоит 1160/365=3,178 у.е. Таким образом высвобождается 3,178×1000=3178 у.е. В результате получается экономия заработной платы в количестве 3178 у.е. Силос, зерно и выпас израсходованы полностью (Х3=Х5=Х6=0). На высвобожденную сумму можно закупить дефицитный силос – 40 т (40×25=1000 у.е.), зерно в количестве 18 т (18×60=1080 у.е.), кроме того, можно взять в аренду дополнительно 15,6 га для выпаса (15,6×70=1092 у.е.).
Финансовая проверка:
1090×25+600×64+38×60+515,6×70+6300×3,18=124064 у.е.
Вложенные в ресурсы деньги остались прежними, следовательно, управление запасами с финансовой точки зрения оказалось верным.
Таким образом, получается новая задача линейного программирования:
Силос 2,1Х1 ≤ 1092;
Комбикорм Х1 + 0,54Х2 ≤ 600;
Зерно 0,6Х2 ≤ 38;
Выпас Х1 ≤ 515,6;
Трудовые ресурсы 10,5Х1 + 2,5Х2 ≤ 6300;
Прибыль F= 40Х1+1Х2 → max.
Ее графическое решение приведено на рис. 8.2, а аналитическое решение симплексным методом – в табл. 8.3.
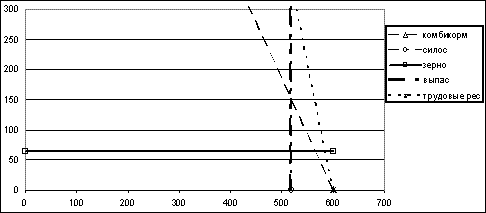
Рис. 8.2. Графическое решение задачи (вторая итерация)
Таблица 8.3
Решение задачи симплексным методом (вторая итерация)
| Базис |
Х1 | Х2 | Х3 | Х4 |
Х5 | Х6 | Х7 |
Aio |
Aio/Air |
| Х3 |
2,1 |
0 |
1 |
0 |
0 |
0 |
0 |
1092 |
∞ |
| Х4 |
1 |
0,5 |
0 |
1 |
0 |
0 |
0 |
600 |
1200 |
| Х5 |
0 |
0,6 |
0 |
0 |
1 |
0 |
0 |
38 |
63,5 |
| Х6 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
515 |
∞ |
| Х7 | 10,5 | 2,5 | 0 | 0 |
0 | 0 | 1 | 6300 | 2520 |
| F | –40 | –1 | 0 | 0 | 0 | 0 | 0 | 0 | |
| Х3 |
2,1 |
0 |
1 |
0 |
0 |
0 |
0 |
1090 |
519 |
| Х4 |
1 |
0 |
0 |
1 |
–0,83 |
0 |
0 |
568,33 |
568,28 |
| Х2 |
0 |
1 |
0 |
0 |
1,67 |
0 |
0 |
63,33 |
∞ |
| Х6 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
515 |
515,55 |
| Х7 | 10,5 | 0 | 0 | 0 |
–4,16 | 0 | 1 | 6141,6 | 584,86 |
| F | –40 | 0 | 0 | 0 |
1,66 | 0 | 0 | 63,58 | |
| Х3 |
0 |
0 |
1 |
0 |
0 |
–2,1 |
0 |
10,5 |
|
| Х4 |
0 |
0 |
0 |
1 |
–0,83 |
–1 |
0 |
50,8 |
|
| Х2 |
0 |
1 |
0 |
0 |
1,66 |
0 |
0 |
63,58 |
|
| Х1 |
1 |
0 |
0 |
0 |
|
1 |
0 |
515,55 |
|
| Х7 | 0 | 0 | 0 | 0 |
–4,17 | –10,5 | 1 | 734,2 | |
| F | 0 | 0 | 0 | 0 | 1,66 | 40 | 0 | 20686 | |
X (515; 63; 10,5; 50,8; 0; 0; 734,2); F=206863.
Х1 округляем в меньшую сторону до ближайшего целого. Это естественно, так как нельзя вырастить 515,65 коровы. Х2 округляем до десятых, так как куриц считаем десятками.
Проверка:
2,1×515+10,5= 1092;
515+ 0,54×63,6 +50,8= 600;
0,6×63,6= 38;
515+0= 515;
10,5×515+ 2,5×63,6 +734,2= 6300;
F=40×515,6+1×63,58=20687.
При имеющихся запасах сырья максимальная прибыль в размере 20686 у.е. может быть получена при производстве 515 коров и 63 десятков куриц. При этом выявлены излишки силоса (Х3=10,5), комбикорма (Х4=50,8) и трудовых ресурсов (Х7=734). Эти ресурсы можно реализовать и докупить на освободившиеся деньги дефицитное зерно и арендовать выпас.
Высвобождаем 700 чел.-дней и продаем 30 т комбикорма. В результате высвобождается 4145 у.е. (700×3,178=2225 у.е. и 30×64=1920 у.е.). На эту сумму мы закупаем дефицитные ресурсы: арендуем еще 36 га выпаса и закупаем 27 т зерна (36×70=2520 и 27×60=1625).
Финансовая проверка:
1090×25+570×64+65,5×60+551×70+5600×3,18=124038 у.е.
Получим новую задачу линейного программирования, решаемую графическим и симплексным методами.
Силос 2,1Х1 ≤ 1090;
Комбикорм Х1 + 0,54Х2 ≤ 570;
Зерно 0,6Х2 ≤ 65;
Выпас Х1 ≤ 551;
Трудовые ресурсы 10,5Х1 + 2,5Х2 ≤ 5600;
Прибыль F= 40Х1+1Х2 → max.
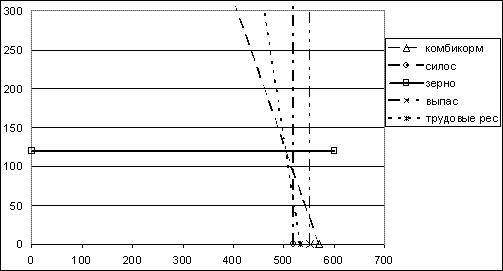
Рис. 8.3. Графическое решение задачи (третья итерация)
Таблица 8.4
Решение задачи симплексным методом (третья итерация)
| Базис |
Х1 | Х2 | Х3 | Х4 |
Х5 | Х6 | Х7 |
Aio |
Aio/Air |
| Х3 |
2,1 |
0 |
1 |
0 |
0 |
0 |
0 |
1090 |
519 |
| Х4 |
1 |
0,5 |
0 |
1 |
0 |
0 |
0 |
570 |
575 |
| Х5 |
0 |
0,6 |
0 |
0 |
1 |
0 |
0 |
65,48 |
∞ |
| Х6 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
551,30 |
551 |
| Х7 | 10,5 | 2,5 | 0 | 0 |
0 | 0 | 1 | 5600 | 533 |
| F | –40 | –1 | 0 | 0 | 0 | 0 | 0 | 0 | |
| Х1 |
1 |
0 |
0,48 |
0 |
0 |
0 |
0 |
519,04 |
∞ |
| Х4 |
0 |
0,5 |
–0,48 |
1 |
0 |
0 |
0 |
50,95 |
102 |
| Х5 |
0 |
0,6 |
0 |
0 |
1 |
0 |
0 |
65,48 |
119 |
| Х6 |
0 |
0 |
–0,48 |
0 |
0 |
1 |
0 |
32,25 |
∞ |
| Х7 | 0 | 2,5 | –5 | 0 |
0 | 0 | 1 | 150 | 60 |
| F | 0 | –7 | 19,0 | 0 |
0 | 0 | 0 | 20762 | |
| Х1 |
1 |
0 |
0,48 |
0 |
0 |
0 |
0 |
519,04 |
|
| Х4 |
0 |
0 |
0,52 |
1 |
0 |
0 |
–0,2 |
20,95 |
|
| Х5 |
0 |
0 |
1,2 |
0 |
1 |
0 |
–0,24 |
29,48 |
|
| Х6 |
0 |
0 |
–0,48 |
0 |
0 |
1 |
0 |
32,25 |
|
| Х2 | 0 | 1 | –2 | 0 |
0 | 0 | 0,4 | 60 | |
| F | 0 | 0 | 17,1 | 0 | 0 | 0 | 0,4 | 20822 | |
X (519; 60; 0; 20; 35; 32; 0); F=20821,9.
При имеющихся запасах сырья максимальная прибыль в размере 83347,62 у.е. может быть получена при производстве 519 коров и 60 десятков куриц. При этом оказываются в дефиците силос и трудовые ресурсы.
Проверка:
2,1×519+0=1090;
519+0,54×60+20=570;
0,6×60+35=65;
519+32=551;
10,5×519+2,5×60+0=5600;
F=40×519+1×60=20821,9.
Анализ переменных свидетельствует об избыточности комбикорма, зерна и выпасных площадей. Продаем 7 т комбикорма, 4 т зерна и 10 га пастбищ отдаем в аренду. При этом освобождаются деньги в сумме 1748 у.е. (7×64+4×60+10×70=1748). На эту сумму закупим дефицитные ресурсы – 17 т силоса и 416 чел.-дней (17×25+416×3,178=1748).
Финансовая проверка:
1190×25+563×64+61×60+541×70+6016×3,18=124368 у.е.
Получим новую задачу линейного программирования, решаемую графическим и симплексным методами.
Силос 2,1Х1 ≤ 1107;
Комбикорм Х1 + 0,54Х2 ≤ 563;
Зерно 0,6Х2 ≤ 61;
Выпас Х1 ≤ 541;
Трудовые ресурсы 10,5Х1 + 2,5Х2 ≤ 6016;
Прибыль F = 40Х1+1Х2 → max.
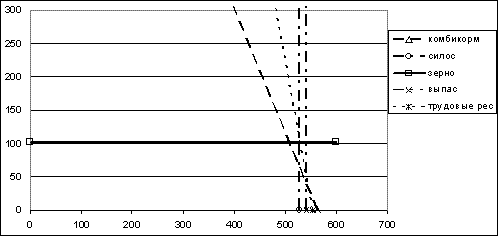
Рис. 8.4. Графическое решение задачи (четвертая итерация)
Таблица 8.5
Решение задачи симплексным методом (четвертая итерация)
| Базис |
Х1 | Х2 | Х3 | Х4 |
Х5 | Х6 | Х7 |
Aio |
Aio/Air |
| Х3 |
2,1 |
0 |
1 |
0 |
0 |
0 |
0 |
1107 |
527 |
| Х4 |
1 |
0,5 |
0 |
1 |
0 |
0 |
0 |
563 |
563 |
| Х5 |
0 |
0,6 |
0 |
0 |
1 |
0 |
0 |
61 |
∞ |
| Х6 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
541 |
541 |
| Х7 | 10,5 | 2,5 | 0 | 0 |
0 | 0 | 1 | 6016 | 554 |
| F | –40 | –1 | 0 | 0 | 0 | 0 | 0 | 0 | |
| Х1 |
1 |
0 |
0,48 |
0 |
0 |
0 |
0 |
527,36 |
∞ |
| Х4 |
0 |
0,5 |
–0,48 |
1 |
0 |
0 |
0 |
35,63 |
71 |
| Х5 |
0 |
0,6 |
0 |
0 |
1 |
0 |
0 |
61,48 |
102 |
| Х6 |
0 |
0 |
–0,48 |
0 |
0 |
1 |
0 |
13,93 |
∞ |
| Х7 | 0 | 2,5 | –5 | 0 |
0 | 0 | 1 | 481,48 | 113 |
| F | 0 | –1 | 19,05 | 0 |
0 | 0 | 0 | 21085,7 | |
| Х1 |
1 |
0 |
0,48 |
0 |
0 |
0 |
0 |
527,36 |
|
| Х2 |
0 |
1 |
–0,95 |
2 |
0 |
0 |
0 |
71,27 |
|
| Х5 |
0 |
0 |
0,57 |
–1,2 |
1 |
0 |
0 |
18,72 |
|
| Х6 |
0 |
0 |
–0,48 |
0 |
0 |
1 |
0 |
13,94 |
|
| Х7 | 0 | 0 | –2,62 | –5 |
0 | 0 | 1 | 303,31 | |
| F | 0 | 0 | 18,1 | 2 | 0 | 0 | 0 | 21157 | |
X (527; 71; 0; 0; 18; 14; 303); F=21157.
Проверка:
2,1×527+0=1107;
527+0,54×71+0=565;
0,6×71+18=61;
527+14=541;
10,5×527+2,5×71+303=6014;
F=40×527+1×71=21151.
Некоторые несовпадения результатов проверок определяются округлением и составляют менее 0,1%.
При имеющихся запасах сырья максимальная прибыль в размере 21157 у.е. может быть получена при производстве 527 коров и 71 десятка куриц. При этом остается недостаток таких ресурсов, как силос и комбикорм.
Анализ переменных свидетельствует об избыточности зерна, выпасных площадей и трудовых ресурсов. Сокращаем трудовые ресурсы на 90 чел.-дней. На освободившуюся сумму 286 у.е. (90×3,178=286) закупим дефицитные ресурсы: 4 т силоса и 3 т комбикорма (4×25+3×64).
Финансовая проверка:
1111×25+566×64+61,5×60+541×70+5926×3,18=124403 у.е.
Получим новую задачу линейного программирования, решаемую графическим и симплексным методами.
Силос 2,1Х1 ≤ 1111;
Комбикорм Х1 + 0,54Х2 ≤ 566;
Зерно 0,6Х2 ≤ 61;
Выпас Х1 ≤ 541;
Трудовые ресурсы 10,5Х1 + 2,5Х2 ≤ 5926;
Прибыль F= 40Х1+1Х2 → max.
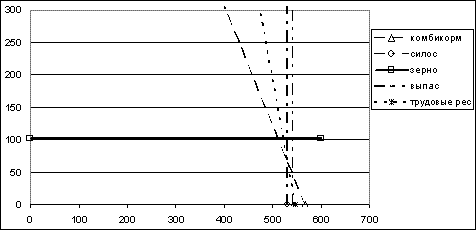
Рис. 8.5. Графическое решение задачи (пятая итерация)
Таблица 8.6
Решение задачи симплексным методом (пятая итерация)
| Базис |
Х1 | Х2 | Х3 | Х4 |
Х5 | Х6 | Х7 |
Aio |
Aio/Air |
| Х3 |
2,1 |
0 |
1 |
0 |
0 |
0 |
0 |
1111,4 |
529 |
| Х4 |
1 |
0,5 |
0 |
1 |
0 |
0 |
0 |
565,91 |
566 |
| Х5 |
0 |
0,6 |
0 |
0 |
1 |
0 |
0 |
61,48 |
∞ |
| Х6 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
541,30 |
541 |
| Х7 | 10,5 | 2,5 | 0 | 0 |
0 | 0 | 1 | 5926 | 546 |
| F | –40 | –1 | 0 | 0 | 0 | 0 | 0 | 0 | |
| Х1 |
1 |
0 |
0,48 |
0 |
0 |
0 |
0 |
529,27 |
∞ |
| Х4 |
0 |
0,5 |
–0,48 |
1 |
0 |
0 |
0 |
36,64 |
73 |
| Х5 |
0 |
0,6 |
0 |
0 |
1 |
0 |
0 |
61,48 |
102 |
| Х6 |
0 |
0 |
–0,48 |
0 |
0 |
1 |
0 |
12,03 |
∞ |
| Х7 | 0 | 2,5 | –5 | 0 |
0 | 0 | 1 | 371 | 148 |
| F | 0 | –1 | 19,0 | 0 |
0 | 0 | 0 | 21171 | |
| Х1 |
1 |
0 |
0,48 |
0 |
0 |
0 |
0 |
529,27 |
|
| Х2 |
0 |
1 |
0,52 |
2 |
0 |
0 |
0 |
73 |
|
| Х5 |
0 |
0 |
1,2 |
–1 |
1 |
0 |
0 |
19,85 |
|
| Х6 |
0 |
0 |
–0,48 |
0 |
0 |
1 |
0 |
12,03 |
|
| Х7 | 0 | 0 | –2 | 5 |
0 | 0 | 1 | 191 | |
| F | 0 | 0 | 18,1 | 2 | 0 | 0 | 0 | 21244 | |
X (529; 73; 0; 2; 20; 12; 191); F=21244.
Проверка:
2,1×529+0=1111;
529+0,54×69+2=566;
0,6×69+20=61;
529+12=541;
10,5×529,27+2,5×69+191=5918;
F=40×529,27+1×73,3=21244.
Финансовая проверка:
1111×25+566×64+61,5×60+541×70+5926×3,18=124403 у.е.
При имеющихся запасах сырья максимальная прибыль в размере 85030,15 может быть получена при выращивании 529 коров и 69 десятков куриц. При этом остается излишек таких ресурсов, как зерно, выпас и трудовые ресурсы. Сокращаем последние на 30 чел.-дней и продаем 5 т зерна. При этом высвобождается 30×3,178+5×60=395 у.е. На эти деньги приобретаем комбикорм в количестве 6 т (395/64).
Получим новую задачу линейного программирования, решаемую графическим и симплексным методами.
Силос 2,1Х1 ≤ 1111;
Комбикорм Х1 + 0,54Х2 ≤ 572;
Зерно 0,6Х2 ≤ 56;
Выпас Х1 ≤ 541;
Трудовые ресурсы 10,5Х1 + 2,5Х2 ≤ 5896;
Прибыль F= 40Х1+1Х2 → max.
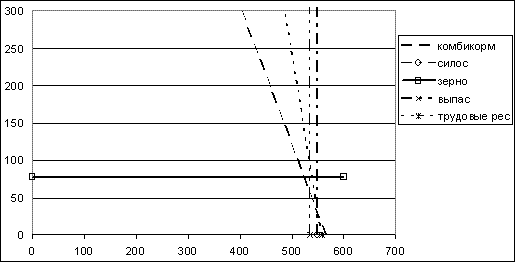
Рис. 8.6. Графическое решение задачи (шестая итерация)
Таблица 8.7
Решение задачи симплексным методом (шестая итерация)
| Базис |
Х1 | Х2 | Х3 | Х4 |
Х5 | Х6 | Х7 |
Aio |
Aio/Air |
| Х3 |
2,1 |
0 |
1 |
0 |
0 |
0 |
0 |
1111 |
529 |
| Х4 |
1 |
0,5 |
0 |
1 |
0 |
0 |
0 |
572 |
572 |
| Х5 |
0 |
0,6 |
0 |
0 |
1 |
0 |
0 |
56 |
∞ |
| Х6 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
541 |
541 |
| Х7 | 10,5 | 2,5 | 0 | 0 |
0 | 0 | 1 | 5896 | 561 |
| F | –40 | –1 | 0 | 0 | 0 | 0 | 0 | 0 | |
| Х1 |
1 |
0 |
0,48 |
0 |
0 |
0 |
0 |
529 |
∞ |
| Х4 |
0 |
0,5 |
–0,48 |
1 |
0 |
0 |
0 |
43 |
86 |
| Х5 |
0 |
0,6 |
0 |
0 |
1 |
0 |
0 |
56 |
93 |
| Х6 |
0 |
0 |
0,48 |
0 |
0 |
1 |
0 |
12 |
∞ |
| Х7 | 0 | 2,5 | 5 | 0 |
0 | 0 | 1 | 341 | 136 |
| F | 0 | –1 | 19 | 0 |
0 | 0 | 0 | 21171 | |
| Х1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
529 |
|
| Х2 |
0 |
1 |
0,48 |
2 |
0 |
0 |
0 |
86 |
|
| Х5 |
0 |
0 |
0,98 |
1,2 |
1 |
0 |
0 |
4 |
|
| Х6 |
0 |
0 |
0,58 |
0 |
0 |
1 |
0 |
12 |
|
| Х7 | 0 | 0 | 2,6 | 5 |
0 | 0 | 1 | 126 | |
| F | 0 | 0 | 18,1 | 10 | 0 | 0 | 0 | 21257 | |
X= (529; 86; 0; 0; 4; 12; 126); F=21257.
Проверка:
2,1×529+0=1111;
529+0,54×86+0=574;
0,6×86+4=56;
529+12=541;
10,5×529+2,5×86+191=5960;
F=40×529+1×86=21246.
Финансовая проверка:
1111×25+572×64+56×60+541×70+5896×3,18=124362 у.е.
При имеющихся запасах сырья максимальная прибыль в размере 21257 у.е. может быть получена при производстве 259 коров и 86 десятков куриц. При этом остается излишек таких ресурсов, как зерно, в количестве 4 т, выпас – 12 га и трудовые ресурсы – 126 чел.-час.
Сокращаем трудовые ресурсы на 70 часов. В результате освобождается 3,178×70=222,5 у.е. На эти деньги закупаем дефицитный силос в количестве 222,5/25=8,9 т.
Получается новая задача линейного программирования:
2,1Х1 ≤ 1120;
Х1 + 0,54Х2 ≤ 572;
0,6Х2 ≤ 56;
Х1 ≤ 541;
10,5Х1 + 2,5Х2 ≤ 5826;
F = 40Х1+1Х2 → max.
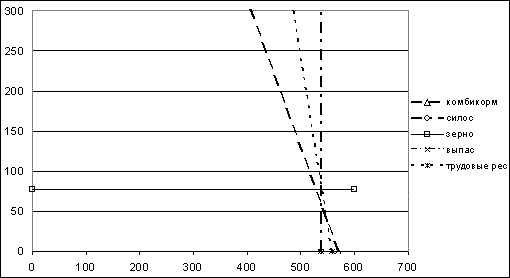
Рис. 8.7. Графическое решение задачи (седьмая итерация)
Таблица 8.8
Решение задачи симплексным методом (седьмая итерация)
| Базис |
Х1 | Х2 | Х3 | Х4 |
Х5 | Х6 | Х7 |
Aio |
Aio/Air |
| Х3 |
2,1 |
0 |
1 |
0 |
0 |
0 |
0 |
1120 |
533 |
| Х4 |
1 |
0,5 |
0 |
1 |
0 |
0 |
0 |
572 |
572 |
| Х5 |
0 |
0,6 |
0 |
0 |
1 |
0 |
0 |
56 |
∞ |
| Х6 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
541 |
541 |
| Х7 | 10,5 | 2,5 | 0 | 0 |
0 | 0 | 1 | 5828 | 555 |
| F | –40 | –1 | 0 | 0 | 0 | 0 | 0 | 0 | |
| Х1 |
1 |
0 |
0,4 |
0 |
0 |
0 |
0 |
533 |
∞ |
| Х4 |
0 |
0,5 |
–0,4 |
1 |
0 |
0 |
0 |
38,67 |
77,3 |
| Х5 |
0 |
0,6 |
0 |
0 |
1 |
0 |
0 |
56 |
93,3 |
| Х6 |
0 |
0 |
–0,4 |
0 |
0 |
1 |
0 |
7,67 |
∞ |
| Х7 | 0 | 2,5 | 4,8 | 0 |
0 | 0 | 1 | 228 | 91 |
| F | 0 | –1 | 19 | 0 |
0 | 0 | 0 | 21333 | |
| Х1 |
1 |
0 |
0,4 |
0 |
0 |
0 |
0 |
533 |
|
| Х2 |
0 |
1 |
8 |
2 |
0 |
0 |
0 |
77,3 |
|
| Х5 |
0 |
0 |
0,48 |
–1,2 |
1 |
0 |
0 |
9,6 |
|
| Х6 |
0 |
0 |
–0,4 |
0 |
0 |
0 |
0 |
7,7 |
|
| Х7 | 0 | 0 | 6,8 | –5 |
0 | 1 | 1 | 34 | |
| F | 0 | 0 | 19,8 | 2 | 0 | 0 | 0 | 21410 | |
X= (533; 77; 0; 0; 9,6 ; 7,7; 34); F=21410.
Проверка:
2,1×533+0=1119;
533+ 0,54×77,3+0=574;
0,6×77,3+9,6=56;
533+8=541;
10,5×533+2,5×77,3+34=5824;
F=40×533+1×77=21400.
При имеющихся запасах сырья максимальная прибыль в размере 21410 у.е. может быть получена при производстве 533 коров и 77 десятков куриц. При этом остается излишек таких ресурсов, как силос – 64 т, зерно – 19 т и трудовые ресурсы – 7,5 чел.-дней.
Продаем силос в количестве 60 т. При этом высвобождается 60×25=1500 у.е. На эту сумму закупим 10 т комбикорма (10×64=640 у.е.) и арендуем дополнительно 12 га выпаса (12×70=840 у.е.).
Новая задача имеет вид:
2,1Х1 ≤ 1140;
Х1 + 0,54Х2 ≤ 582;
0,6Х2 ≤ 56;
Х1 ≤ 553;
10,5Х1 + 2,5Х2 ≤ 5826;
F= 160Х1+5Х2 &$8594; max.
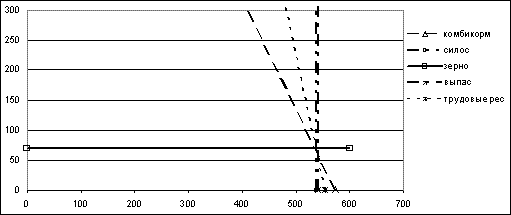
Рис. 8.8. Графическое решение задачи (восьмая итерация)
Таблица 8.9
Решение задачи симплексным методом (восьмая итерация)
| Базис |
Х1 | Х2 | Х3 | Х4 |
Х5 | Х6 | Х7 |
Aio |
Aio/Air |
| Х3 |
2,1 |
0 |
1 |
0 |
0 |
0 |
0 |
1140 |
543 |
| Х4 |
1 |
0,5 |
0 |
1 |
0 |
0 |
0 |
582 |
582 |
| Х5 |
0 |
0,6 |
0 |
0 |
1 |
0 |
0 |
56 |
∞ |
| Х6 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
553 |
553 |
| Х7 | 10,5 | 2,5 | 0 | 0 |
0 | 0 | 1 | 5837 | 555 |
| F | –40 | –1 | 0 | 0 | 0 | 0 | 0 | 0 | |
| Х1 |
1 |
0 |
0,48 |
0 |
0 |
0 |
0 |
543 |
∞ |
| Х4 |
0 |
0,5 |
–0,48 |
1 |
0 |
0 |
0 |
39,14 |
78 |
| Х5 |
0 |
0,6 |
0 |
0 |
1 |
0 |
0 |
56 |
93 |
| Х6 |
0 |
0 |
–0,48 |
0 |
0 |
1 |
0 |
10,14 |
∞ |
| Х7 | 0 | 2,5 | 50 | 0 |
0 | 0 | 1 | 137 | 54 |
| F | 0 | –1 | 19 | 0 |
0 | 0 | 0 | 21714 | |
| Х1 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
543 |
|
| Х4 |
0 |
0 |
–1 |
1 |
0 |
0 |
0 |
11,7 |
|
| Х5 |
0 |
0 |
0,58 |
0 |
1 |
0 |
0 |
23 |
|
| Х6 |
0 |
0 |
–0,48 |
0 |
0 |
1 |
0 |
10,1 |
|
| Х2 | 0 | 1 | 52 | 0 |
0 | 0 | 1 | 54 | |
| F | 0 | 0 | 81 | 0 | 0 | 0 | 0 | 21774 | |
X=(543; 54; 0; 11,7; 23; 10,1; 0); F=21774.
Проверка:
2,1×543+0= 1140;
543+ 0,54×54 +0=572;
0,6×54+23=55,4;
543+10= 553;
10,5×543+ 2,5×54+0=5836;
F=40×543+1×54=21774.
При имеющихся запасах сырья прибыль в размере 21774 может быть получена при производстве 54 коров и 54 десятков куриц. Продаем 10 т зерна, 5 т комбикорма и уменьшаем площадь арендуемого выпаса на 5 га. Освободившиеся деньги: 10×60+5×64+5×70=1270 у.е. На них приобретаем 24 т силоса и увеличиваем трудовые ресурсы на 47 чел.-часов (24×25+210×3,178=12676 у. е.).
Силос 2,1Х1 ≤ 1164;
Комбикорм Х1 + 0,54Х2 ≤ 577;
Зерно 0,6Х2 ≤ 46;
Выпас Х1 ≤ 548;
Трудовые ресурсы 10,5Х1 + 2,5Х2 ≤ 5873;
Прибыль F= 40Х1+1Х2 → max.
Начиная с этой итерации, графический метод не используем, так как при незначительных изменениях запасов ресурсов он не нагляден.
Таблица 8.10
Решение задачи симплексным методом (девятая итерация)
| Базис |
Х1 | Х2 | Х3 | Х4 |
Х5 | Х6 | Х7 |
Aio |
Aio/Air |
| Х3 |
2,1 |
0 |
1 |
0 |
0 |
0 |
0 |
1164 |
554 |
| Х4 |
1 |
0,5 |
0 |
1 |
0 |
0 |
0 |
577 |
577 |
| Х5 |
0 |
0,6 |
0 |
0 |
1 |
0 |
0 |
46 |
∞ |
| Х6 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
548 |
548 |
| Х7 | 10,5 | 2,5 | 0 | 0 |
0 | 0 | 1 | 5873 | 559 |
| F | –160 | –5 | 0 | 0 | 0 | 0 | 0 | 0 | |
| Х3 |
0 |
0 |
1 |
0 |
0 |
–2,1 |
0 |
13,2 |
∞ |
| Х4 |
0 |
0,5 |
0 |
1 |
0 |
1 |
0 |
29 |
14,5 |
| Х5 |
0 |
0,6 |
0 |
0 |
1 |
0 |
0 |
46 |
77 |
| Х1 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
548 |
∞ |
| Х7 | 0 | 2,5 | 0 | 0 |
0 | –10,5 | 1 | 119 | 48 |
| F | 0 | –5 | 0 | 0 |
0 | 160 | 0 | 87680 | |
| Х3 |
0 |
0 |
0,48 |
0 |
0 |
0 |
0 |
13 |
|
| Х4 |
0 |
0 |
0,5 |
1 |
0 |
0 |
0 |
5 |
|
| Х5 |
0 |
0 |
1,2 |
0 |
1 |
0 |
0 |
17,4 |
|
| Х1 |
1 |
0 |
–0,48 |
0 |
0 |
1 |
0 |
548 |
|
| Х2 | 0 | 1 | 2 | 0 |
0 | 0 | 1 | 48 | |
| F | 0 | 0 | 97,2 | 10 | 0 | 0 | 0 | 87918 | |
X=(548; 48; 13; 4; 0; 0); F=87918.
Проверка:
2,1×548+13=11648;
548+ 0,54×48+5=578
0,6×48+17,4=46
548+0=548;
10,5×548+2,5×48+0=5874;
F=160×548+5×48=87920.
Ошибки составляют менее 1%. Однако еще есть значительные излишки зерна Х5=17,4 т, составляющие (46–17)/46×100=63% от имеющихся запасов. В дефиците же на данной итерации оказываются выпас и трудовые ресурсы.
Продаем 15 т зерна (15×60=900 у.е.) и приобретаем на освободившиеся деньги 10 га выпаса (10×70=700 у.е.) и 63 чел.-дней (63×3,178=200 у.е.).
Новая задача имеет вид:
2,1Х1 ≤ 1164;
Х1 + 0,54Х2 ≤ 577;
0,6Х2 ≤ 31;
Х1 ≤ 558;
10,5Х1 + 2,5Х2 ≤ 6036;
F= 160Х1+5Х2 → max.
Таблица 8.11
Решение задачи симплексным методом (десятая итерация)
| Базис |
Х1 | Х2 | Х3 | Х4 |
Х5 | Х6 | Х7 |
Aio |
Aio/Air |
| Х3 |
2,1 |
0 |
1 |
0 |
0 |
0 |
0 |
1164 |
554 |
| Х4 |
1 |
0,54 |
0 |
1 |
0 |
0 |
0 |
577 |
577 |
| Х5 |
0 |
0,6 |
0 |
0 |
1 |
0 |
0 |
31 |
∞ |
| Х6 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
558 |
558 |
| Х7 | 10,5 | 2,5 | 0 | 0 |
0 | 0 | 1 | 6036 | 575 |
| F | –160 | –5 | 0 | 0 | 0 | 0 | 0 | 0 | |
| Х3 |
0 |
0 |
1 |
0 |
0 |
–2,1 |
0 |
7,8 |
∞ |
| Х4 |
0 |
0,54 |
0 |
1 |
0 |
1 |
0 |
19 |
35 |
| Х5 |
0 |
0,6 |
0 |
0 |
1 |
0 |
0 |
31 |
52 |
| Х1 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
558 |
∞ |
| Х7 | 0 | 2,5 | 0 | 0 |
0 | –10,5 | 1 | 177 | 70,8 |
| F | 0 | –5 | 0 | 0 |
0 | 160 | 0 | 89280 | |
| Х3 |
0 |
0 |
0,48 |
0 |
0 |
0 |
|
4,2 |
|
| Х2 |
0 |
1 |
0,5 |
1 |
0 |
0 |
|
35 |
|
| Х5 |
0 |
0 |
1,2 |
0 |
1 |
0 |
|
9,9 |
|
| Х1 |
1 |
0 |
–0,48 |
0 |
0 |
1 |
|
558 |
|
| Х7 | 0 | 0 | 2 | 0 |
0 | 0 | | 89 | |
| F | 0 | 0 | 97,2 | 10 | 0 | 0 | | 89490 | |
X=(558; 35; 4,2; 0; 9,9; 0; 89); F=89490.
Проверка:
2,1×558+4=1176;
558+0,54×35+0=577;
0,6×35+10=31;
558+0=558;
10,5×558+ 2,5×35+89=6035,5;
F=160×558+5×35=89455.
Еще есть излишки зерна Х5=9,9 т, составляющие (31–9,7)/31×100=69% от имеющихся запасов. В дефиците же на данной итерации оказываются комбикорм и выпас.
Продаем 7 т зерна (7×50=900 у.е.) и на освободившиеся деньги приобретаем 10 га выпаса (10×70=700 у.е.) и 63 чел.-дней (63×3,178=200 у.е.).
Новая задача имеет вид:
2,1Х1 ≤ 1164;
Х1 + 0,54Х2 ≤ 577;
0,6Х2 ≤ 24;
Х1 ≤ 568;
10,5Х1 + 2,5Х2 ≤ 6089
F= 160Х1+5Х2 → max.
Таблица 8.12
Решение задачи симплексным методом (одиннадцатая итерация)
| Базис |
Х1 | Х2 | Х3 | Х4 |
Х5 | Х6 | Х7 |
Aio |
Aio/Air |
| Х3 |
2,1 |
0 |
1 |
0 |
0 |
0 |
0 |
1169 |
557 |
| Х4 |
1 |
0,54 |
0 |
1 |
0 |
0 |
0 |
580,5 |
580,5 |
| Х5 |
0 |
0,6 |
0 |
0 |
1 |
0 |
0 |
17 |
∞ |
| Х6 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
578 |
578 |
| Х7 | 10,5 | 2,5 | 0 | 0 |
0 | 0 | 1 | 5989 | 580 |
| F | –160 | –5 | 0 | 0 | 0 | 0 | 0 | 0 | |
| Х1 |
1 |
0 |
0,48 |
0 |
0 |
0 |
0 |
557 |
∞ |
| Х4 |
0 |
0,54 |
–0,48 |
1 |
0 |
0 |
0 |
28 |
46 |
| Х5 |
0 |
0,6 |
0 |
0 |
1 |
0 |
0 |
17 |
28 |
| Х6 |
0 |
0 |
–0,48 |
0 |
0 |
1 |
0 |
21 |
∞ |
| Х7 | 0 | 2,5 | –5 | 0 |
0 | 0 | 1 | 144 | 57 |
| F | 0 | –5 | 76 | 0 |
0 | 0 | 0 | 88686 | |
| Х1 |
1 |
0 |
0,48 |
0 |
0 |
0 |
0 |
554 |
|
| Х4 |
0 |
0 |
–0,48 |
1 |
0,9 |
0 |
0 |
1,1 |
|
| Х2 |
0 |
1 |
0 |
0 |
1,7 |
0 |
0 |
40 |
|
| Х6 |
0 |
0 |
–0,48 |
0 |
0 |
1 |
0 |
13,6 |
|
| Х7 | 0 | 0 | –5 | 0 |
4,2 | 0 | 1 | 169 | |
| F | 0 | 0 | 76 | 10 | 8,3 | 0 | 0 | 88886 | |
X=(554; 40; 0; 1,1; 0; 13,6; 169); F=88886.
Проверка:
2,1×554+4×0=1163;
554+0,54×40+1=577;
0,6×40+0=24;
554+14=568;
10,5×554+ 2,5×40+169=6086;
F=160×554+5×40=88840.
Сдаем в аренду 10 га выпаса (10×70=700 у.е.) и сокращаем трудовые ресурсы на 100 чел.-дней (100×3,178=318 у.е.) и приобретаем на освободившиеся деньги 9,5 т силоса (9,5×25=237 у.е.) и 13 т зерна (13×60=780 у.е.).
Новая задача имеет вид:
2,1Х1 ≤ 1169;
Х1 + 0,54Х2 ≤ 580,5;
0,6Х2 ≤ 30;
Х1≤ 568;
10,5Х1 + 2,5Х2 ≤ 5889
F= 160Х1+5Х2 → max.
Таблица 8.13
Решение задачи симплексным методом (двенадцатая итерация)
| Базис |
Х1 | Х2 | Х3 | Х4 |
Х5 | Х6 | Х7 |
Aio |
Aio/Air |
| Х3 |
2,1 |
0 |
1 |
0 |
0 |
0 |
|
1169 |
556,7 |
| Х4 |
1 |
0,54 |
0 |
1 |
0 |
0 |
|
580,5 |
580,5 |
| Х5 |
0 |
0,6 |
0 |
0 |
1 |
0 |
|
30 |
∞ |
| Х6 |
1 |
0 |
0 |
0 |
0 |
1 |
|
568 |
568 |
| Х7 | 10,5 | 2,5 | 0 | 0 |
0 | 0 | | 5889 | 560,9 |
| F | –160 | –5 | 0 | 0 | 0 | 0 | | 0 | |
| Х1 |
1 |
0 |
0,5 |
0 |
0 |
0 |
|
556,7 |
∞ |
| Х4 |
0 |
0,54 |
–0,5 |
1 |
0 |
0 |
|
23,8 |
– |
| Х5 |
0 |
0,6 |
0 |
0 |
1 |
0 |
|
30 |
50 |
| Х6 |
0 |
0 |
–0,5 |
0 |
0 |
1 |
|
11,3 |
– |
| Х7 | 0 | 2,5 | 0 | 0 |
0 | 0 | | 44 | 2805 |
| F | 0 | –5 | 76 | 0 |
0 | 0 | | 8967 | |
| Х1 |
1 |
0 |
0,5 |
0 |
0 |
0 |
|
556,7 |
|
| Х4 |
0 |
0 |
–0,5 |
1 |
0 |
0 |
|
3,2 |
|
| Х2 |
0 |
1 |
0 |
0 |
1 |
0 |
|
50 |
|
| Х6 |
0 |
0 |
–0,5 |
0 |
0 |
1 |
|
11,3 |
|
| Х7 | 0 | 0 | 0 | 0 |
0 | 0 | | 81 | |
| F | 0 | 0 | 76 | 0 | 2,4 |
0 | | 89322 | |
X=(556,7; 50; 0; 3,2; 0; 11,3; 81); F=89322.
Проверка:
2,1×556,7+0=1169;
556,7+0,54×50+3,2=586,9;
0,6×50+0=30;
556,7+11,3=568;
10,5×556,7+2,5×50+81=6086;
F=160×556,7+5×50=89322.
На этом этапе можно считать задачу завершенной, так как остатки ресурсов не превышают 1% от их запасов.
|