МОДУЛЬ 2. Основы статистической обработки опытных данных

Тема 2.1. Основы статистической обработки опытных данных в агрономических исследованиях. Статистические характеристики количественной и качественной изменчивости

План.

1. Основы статистики
2. Статистические характеристики количественной изменчивости
3. Типы статистического распределения
4. Методы проверки статистических гипотез

1. Основы статистики

Окружающий нас мир насыщен информацией - разнообразные потоки данных окружают нас, захватывая в поле своего действия, лишая правильного восприятия действительности. Не будет преувеличением сказать, что информация становится частью действительности и нашего сознания.

Без адекватных технологий анализа данных человек оказывается беспомощным в жестокой информационной среде и скорее напоминает броуновскую частицу, испытывающую жесткие удары со стороны и не имеющую возможности рационально принять решение.

Статистика позволяет компактно описать данные, понять их структуру, провести классификацию, увидеть закономерности в хаосе случайных явлений. Даже простейшие методы визуального и разведочного анализа данных позволяют существенно прояснить сложную ситуацию, первоначально поражающую нагромождением цифр.

Статистическое описание совокупности объектов занимает промежуточное положение между индивидуальным описанием каждого из объектов совокупности, с одной стороны, и описанием совокупности по её общим свойствам, совсем не требующим её расчленения на отдельные объекты, - с другой. По сравнению с первым способом статистические данные всегда в большей или меньшей степени обезличены и имеют лишь ограниченную ценность в случаях, когда существенны именно индивидуальные данные (например, учитель, знакомясь с классом, получит лишь весьма предварительную ориентировку о положении дела из одной статистики числа выставленных его предшественником отличных, хороших, удовлетворительных и неудовлетворительных оценок). С другой стороны, по сравнению с данными о наблюдаемых извне суммарных свойствах совокупности статистические данные позволяют глубже проникнуть в существо дела. Например, данные гранулометрического анализа породы (то есть данные о распределении образующих породу частиц по размерам) дают ценную дополнительную информацию по сравнению с испытанием нерасчленённых образцов породы, позволяя в некоторой мере объяснить свойства породы, условия её образования и прочее.

Метод исследования, опирающийся на рассмотрение статистических данных о тех или иных совокупностях объектов, называется статистическим. Статистический метод применяется в самых различных областях знания. Однако черты статистического метода в применении к объектам различной природы столь своеобразны, что было бы бессмысленно объединять, например, социально-экономическую статистику, физическую статистику.

Общие черты статистического метода в различных областях знания сводятся к подсчёту числа объектов, входящих в те или иные группы, рассмотрению распределения количеств, признаков, применению выборочного метода (в случаях, когда детальное исследование всех объектов обширной совокупности затруднительно), использованию теории вероятностей при оценке достаточности числа наблюдений для тех или иных выводов и т. п. Эта формальная математическая сторона статистических методов исследования, безразличная к специфической природе изучаемых объектов, и составляет предмет математическая статистика

Связь математической статистики с теорией вероятностей имеет в разных случаях различный характер. Теория вероятностей изучает не любые явления, а явления случайные и именно «вероятностно случайные», то есть такие, для которых имеет смысл говорить о соответствующих им распределениях вероятностей. Тем не менее, теория вероятностей играет определённую роль и при статистическом изучении массовых явлений любой природы, которые могут не относиться к категории вероятностно случайных. Это осуществляется через основанные на теории вероятностей теорию выборочного метода и теорию ошибок измерений. В этих случаях вероятностным закономерностям подчинены не сами изучаемые явления, а приёмы их исследования.

Более важную роль играет теория вероятностей при статистическом исследовании вероятностных явлений. Здесь в полной мере находят применение такие основанные на теории вероятностей разделы математической статистики, как теория статистической проверки вероятностных гипотез, теория статистической оценки распределений вероятностей и входящих в них параметров и так далее. Область же применения этих более глубоких статистических методов значительно уже, так как здесь требуется, чтобы сами изучаемые явления были подчинены достаточно определённым вероятностным закономерностям.

Вероятностные закономерности получают статистическое выражение (вероятности осуществляются приближённо в виде частот, а математические ожидания - в виде средних) в силу больших чисел закона.

Чтобы выявить и оценить лучшие агротехнические приемы и сорта, изучаемые в полевом опыте, применяют статистическую обработку данных опыта, представленных в виде поделяночных числовых показателей урожайности и других свойств и качеств подопытных растений. Эти показатели характеризуют изучаемое явление и отражают результат действия исследуемых факторов, проявившихся в конкретном месте за определенный период времени, со всеми искажениями, отступлениями от истинных данных вследствие различных причин, наблюдавшихся во время проведения опыта.

Статистика в широком понимании может быть определена как наука о количественном анализе массовых явлений природы и общества, служащем для выявления их качественных своеобразий.

Статистикой называется отрасль знаний, объединяющая принципы и методы с числовыми данными, характеризующими массовые явления. В этом смысле статистика включает в себя нескольких самостоятельных дисциплин: общую теорию статистики как вводный курс, теорию вероятностей и математическую статистику как науки об основных категориях и математических свойствах генеральной совокупности и их выборочных оценках.

Слово «статистика» происходит от латинского слова status - состояние, положение вещей. Первоначально оно употребляется в значении «политическое состояние». Отсюда итальянское слово stato – государство и statista – знаток государства. В научный обиход слово «статистика» вошло в 18 веке и первоначально употреблялось как «государствоведение».

В настоящее время статистика может быть определена как собирание массовых данных, их обобщение, представление, анализ и интерпретация. Это особый метод, который используется в различных сферах деятельности, в решении разнообразных задач.

Статистика позволяет выявить и измерить закономерности развития социально-экономических явлений и процессов, взаимосвязи между ними. Познание закономерностей возможно только в том случае, если изучаются не отдельные явления, а совокупности явлений, поскольку закономерности проявляются в полной мере, лишь в массе явлений. В каждом отдельном явлении необходимое – то, что присуще всем явлениям данного вида, проявляется в единстве со случайным, индивидуальным, присущим лишь этому конкретному явлению.

Закономерности, в которых необходимость неразрывно связана в каждом отдельном явлении со случайностью и лишь во множестве явлений проявляет себя закон, называются статистическими.

Соответственно предметом статистического изучения всегда выступают совокупности тех или иных явлений, включающие все множество проявлений исследуемой закономерности. В большой совокупности индивидуальные разнообразия взаимнопогашаются, и на первый план выходят закономерные свойства. Поскольку статистика призвана выявлять закономерное, она, опираясь на данные о каждом отдельном проявлении изучаемой закономерности, обобщает их и таким образом получает количественное выражение этой закономерности.

Каждый шаг исследования завершается интерпретацией полученных результатов: какое заключение можно сделать исходя из проведенного анализа, что говорят цифры – подтверждают ли они исходные предположения или открывают что-то новое? Интерпретация данных ограничена исходным материалом. Если заключения основаны на данных выборки, то она должна быть репрезентативной, чтобы выводы были отнесены к совокупности в целом. Статистика позволяет выяснить все то полезное, что содержится в исходных данных и определить, что и как можно использовать в принятии решений.

Термин вариационная статистика был введен в 1899году Дункером для обозначения методов математической статистики, применяемых при изучении некоторых биологических явлений. Несколько ранее, в 1889 году, Ф. Гальтоном был введен другой термин – биометрия (от греческих слов «биос» - жизнь и «метрейн» - измерять), обозначавший применение некоторых методов математической статистики при изучении наследственности, изменчивости и других биологических явлений. Основываясь на теории вероятностей, вариационная статистика позволяет правильно подойти к анализу количественного выражения изучаемых явлений, дать критическую оценку достоверности полученных количественных показателей, установить характер связи между изучаемыми явлениями, а, следовательно, понять их качественное своеобразие.

Важно помнить, что всякий биологический объект обладает изменчивостью. Т.е. каждый из признаков (высота растений, число зерен в колосе, содержание элементов питания) у различных особей может иметь различную степень выраженности, что свидетельствует о колеблемости или варьировании признака.

При статистическом методе исследования внимание сосредоточено не на отдельном объекте, а на группе однородных объектов, т.е. на некоторой их совокупности, объединенных для совместного изучения. Некоторое количество однородных единиц, расположенных по какому-либо одному или нескольким изменяющимся признакам, называется статистической совокупностью.

Статистические совокупности делятся на:

1. генеральные
2. выборочные

Генеральная совокупность объединяет все возможные изучаемые однородные единицы, например, растения на поле, популяции вредителей на поле, возбудители болезней растений. Выборочная совокупность представляет собой некоторую часть единиц, взятых из общей совокупности и попавших на проверку. При изучении, например, урожайности яблонь определенного сорта генеральную совокупность представляют все деревья данного сорта, возраста, произрастающие в определенных однородных условиях. Выборочная совокупность состоит из некоторого количества деревьев яблони, взятых на пробных площадках в изучаемых насаждениях.

Совершенно очевидно, что при статистических исследованиях приходится иметь дело исключительно с выборочными совокупностями. Правильность суждений о свойствах генеральной совокупности на основании анализа выборочной совокупности, прежде всего, зависит от ее типичности. Таким образом, чтобы выборка действительно отражала характерные свойства генеральной совокупности, выборочная совокупность должна объединять достаточное количество однородных единиц, обладающих свойством репрезентативности. Репрезентативность достигается случайным отбором вариант из генеральной совокупности, что обеспечивает равную возможность для всех членов генеральной совокупности попасть в состав выборки.

Статистическое изучение тех или иных явлений в своей основе имеет анализ изменчивости показателей или величин, входящих в состав статистических совокупностей. Статистические величины могут принимать разные значения, обнаруживая при этом в своей изменчивости некоторую закономерность. В связи с этим статистические величины можно определить как величины, принимающие различные значения с определенными вероятностями.

В процессе наблюдений или проведения опытов мы сталкиваемся с различными по своему роду изменчивыми показателями. Одни из них носят ярко выраженный количественный характер и легко поддаются измерениям, другие же не могут быть выражены обычным количественным путем и носят типичный качественный характер.

В связи с этим различают два типа изменчивости или варьирования:

1. количественная
2. качественная

2. Статистические характеристики количественной изменчивости

В качестве примера количественной изменчивости следует отнести: изменчивость количества колосков в колосе пшеницы, изменчивость размеров и веса семян, содержания в них жиров, белков и т.д. Примером качественного варьирования служат: изменение окраски или опушенности различных органов растения, гладкий и морщинистый горох, обладающий зеленой или желтой окраской, различная степень пораженности растений болезнями и вредителями.

Количественное варьирование в свою очередь может быть разделено на два рода: варьирование непрерывное и прерывистое.

Непрерывное варьирование объединяет случаи, когда изучаемые совокупности состоят из статистических единиц, определяемых измерениями или вычислением на основе этих измерений. Примером непрерывного варьирования можно выразить: вес и размеры семян, длина междоузлий, урожайность сельскохозяйственных культур. Во всех этих случаях изучаемые количественные показатели теоретически могут принимать все возможные значения, как целые, так и дробные между крайними своими пределами. Переход от крайнего минимального значения к максимальному теоретически является постепенным и может быть представлен сплошной линией.

При прерывистом варьировании отдельные статистические величины представляют собой совокупность отдельных элементов, выражаемую уже не измерением и не вычислением, а счетом. Примером такого варьирования могут служить изменение числа семян в плодах, числа лепестков в цветке, числа деревьев на единице площади, числа початков кукурузы на одном растении. Такого типа прерывистые варьирования называются также иногда целыми, потому, что отдельные статистические величины приобретают вполне определенные целые значения, в то время как при непрерывном варьировании эти величины могут выражаться и целыми, и дробными значениями.

Основными статистическими характеристиками количественной изменчивости являются следующие:

1.Средняя арифметическая;

Показатели изменчивости признака:

2. дисперсия;

3. стандартное отклонение;

4. коэффициент вариации;

5. Стандартная ошибка средней арифметической;

6. Относительная ошибка.

Cреднее арифметическое. При изучении варьирущих количественных показателей основной сводной величиной является их среднее арифметическое значение. Среднее арифметическое служит как для суждения об отдельных изучаемых совокупностях, так и для сравнения соответствующих совокупностей друг с другом. Полученные средние значения являются основой для построения выводов и для разрешения тех или иных практических вопросов.

Для вычисления среднего арифметического используют следующую формулу: если сумму всех вариант (x₁ + x₂ + … + x_n) обозначить через Σ x_i , число вариантов - через n, то средняя арифметическая определяется:

x_ср.=Σ x_i/ n)

Среднее арифметическое дает первую общую количественную характеристику изучаемой статистической совокупности. При разрешении ряда теоретических и практических вопросов, наряду со знанием среднего значения анализируемого показателя, возникает необходимость в дополнительном установлении характера распределения вариант около этого среднего.

Объктам сельскохозяйственных и биологических исследований свойственна изменчивость признаков и свойств во времени и в пространстве. Причинами ее являются как внутренние, наследственные особенности организмов, так и различная норма их реакции на условия внешней среды.

Выявление характера рассеяния – одна из основных задач статистического анализа опытных данных, который позволяет не только оценить степень разброса наблюдений, но и использовать эту оценку для анализа и интерпретации результатов исследования.

Характер группировки вариант около их среднего значения, называемый также рассеянием, может служить показателем степени изменчивости изучаемого материала. Показатели изменчивости. Лимиты (размах варьирования) – это минимальное и максимальное значения признака в совокупности. Чем больше разность между ними, тем изменчивее признак.

Дисперсия S² и стандартное отклонение S. Эти статистические характеристики являются основными мерами вариации (рассеяния) изучаемого признака. Дисперсия (средний квадрат) – это частное от деления суммы квадратов отклонений Σ (x –x) ² на число всех измерений без единицы:

Σ (x – x) ² / n -1

Стандартное, или среднее квадратическое, отклонение получают путем извлечения квадратного корня из дисперсии:

S = √ S²

Стандартное отклонение характеризует собой степень изменчивости изучаемого материала, меру степени влияния на признак различных второстепенных причин его варьирования, выраженных в абсолютных мерах, т.е. в тех же единицах измерения, что и отдельные значения вариант. В связи с этим стандартное отклонение может быть использовано только при сравнении изменчивости статистических совокупностей, варианты которых выражены в одинаковых единицах измерения.

В статистике принято считать, что диапазон изменчивости в совокупностях достаточно большого объема, которые находятся под постоянным влиянием множества разнообразных и разнонаправленных факторов (биологические явления), не выходят за пределы 3S от среднего арифметического значения. О таких совокупностях говорят, что они подчиняются нормальному распределению вариант.

Ввиду того, что диапазон изменчивости для каждой исследуемой биологической совокупности находится в пределах 3S от среднего арифметического, то чем больше величина стандартного отклонения, тем больше изменчивость признака в исследуемых совокупностях. Стандартное отклонение используется как самостоятельный показатель, так и в качестве основы для вычисления других показателей.

При сравнении изменчивости разнородных совокупностей необходимо пользоваться мерой варьирования, представляющей собой отвлеченное число. Для этой цели в статистике введен коэффициент вариации, под которым понимают стандартное отклонение, выраженное в процентах к средней арифметической данной совокупности:

V = S / x × 100%.

Коэффициент вариации позволяет дать объективную оценку степени варьирования при сравнении любых совокупностей. При изучении количественных признаков он позволяет выделить из них наиболее устойчивые. Изменчивость считают незначительной, если коэффициент вариации не превышает 10%, средней – если он от 10% до 20%, и значительной – если он более 20%.

На основании рассмотренных показателей приходим к суждению о качественном своеобразии всей генеральной совокупности. Очевидно, что степень надежности наших суждений о генеральной совокупности будет зависеть, прежде всего, от того, насколько в той или иной части выборочной совокупности ее индивидуальные, а также случайные особенности не мешают проявлению общих закономерностей и свойств изучаемого явления.

В связи с тем, что при проведении опытных работ и научных исследований в большинстве случаев мы не можем оперировать с очень большими по численному составу выборками, то возникает необходимость определения возможных ошибок в наших характеристиках изучаемого материала на основе этих выборок. Необходимо отметить, что под ошибками в данном случае следует понимать не погрешности в вычислениях тех или иных статистических показателей, а пределы возможных колебаний их значений по отношению ко всей совокупности.

Сопоставление отдельных найденных значений статистических показателей с возможными пределами их отклонений и служит, в конечном счете, критерием оценки надежности для полученных выборочных характеристик. Разрешение этого важного как в теоретическом, так и в практическом отношениях вопроса дает теория статистических ошибок.

Подобно тому, как распределяются варианты вариационного ряда около своего среднего, так же будут распределяться и частные значения средних, полученных из отдельных выборок. Т. е., чем сильнее будут варьировать изучаемые объекты, тем сильнее будут варьировать и частные значения. Вместе с тем, чем на большем числе вариант будут получены частные значения средних, тем ближе они будут к истинному значению среднего арифметического всей статистической совокупности. На основании выше изложенного ошибка выборочной средней (стандартная ошибка) является мерой отклонения выборочной средней от средней генеральной совокупности. Ошибки выборки возникают в результате неполной репрезентативности выборочной совокупности, а также при перенесении данных, полученных при изучении выборки, на всю генеральную совокупность. Величина ошибки зависит от степени изменчивости изучаемого признака и объема выборки.

Стандартная ошибка прямо пропорциональна выборочному стандартному отклонению и обратно пропорциональна корню квадратному из числа измерений:

S_X = S / √ n

Ошибки выборки выражают в тех же единицах измерения, что и варьирующий признак и показывает те пределы, в которых может заключаться истинное значение среднего арифметического изучаемой генеральной совокупности. Абсолютная ошибка выборочной средней используется для установления доверительных границ в генеральной совокупности, достоверности выборочных показателей и разности, а также для установления объема выборки в научно-исследовательской работе.

Ошибка среднего может быть использована для получения показателя точности исследования - относительной ошибки выборочной средней. Это ошибка выборки, выраженная в процентах от соответствующей средней:

S_X, % = S_x / x_ср × 100

Результаты считаются вполне удовлетворительными, если величина относительной ошибки не превышает 3-5% и соответствует удовлетворительному уровню, при 1-2% - очень высокая точность, 2-3% - высокая точность.

3. Типы статистического распределения

Частота проявления определенных значений признака в совокупности называется распределением. Различают эмпирические и теоретические распределения частот совокупности результатов наблюдений. Эмпирическое распределение – это распределение результатов измерений, полученных при изучении выборки. Теоретическое распределение предполагает распределение измерений на основании теории вероятностей. К их числу относятся: нормальное (Гауссово) распределение, распределение Стьюдента (t – распределение), F – распределение, распределение Пуассона, биноминальное.

Наибольшее значение в биологических исследованиях имеет нормальное или Гауссово распределение – это совокупность измерений, в котором варианты группируются вокруг центра распределения и их частоты равномерно убывают вправо и влево от центра распределения (x). Отдельные варианты отклоняются от средней арифметической симметрично, и размах вариации в обе стороны не превышает 3 σ . Нормальное распределение характерно для совокупностей, на членов которых суммарно влияет бесконечно большое количество разнообразных и разнонаправленных факторов. Каждый фактор вносит определенную часть в общую изменчивость признака. Бесконечные колебания факторов обусловливают изменчивость отдельных членов совокупностей.

Данный критерий был разработан Уильямом Госсеттом для оценки качества пива в компании Гиннесс. В связи с обязательствами перед компанией по неразглашению коммерческой тайны (а руководство Гиннесса считало таковой использование статистического аппарата в своей работе), статья Госсетта вышла в журнале «Биометрика» под псевдонимом «Student» (Студент).

Для применения данного критерия необходимо, чтобы исходные данные имели нормальное распределение. В случае применения двухвыборочного критерия для независимых выборок также необходимо соблюдение условия равенства дисперсий. Существуют, однако, альтернативы критерию Стьюдента для ситуации с неравными дисперсиями.

В реальных исследованиях некорректное использование критерия Стьюдента осложняется также и тем, что подавляющее большинство исследователей не только не проверяют гипотезу о равенстве генеральных дисперсий, но не выполняют проверку и первого ограничения: нормальности в обеих сравниваемых группах. В итоге авторы таких публикаций вводят в заблуждение относительно истинных результатов проверки равенства средних как себя, так и своих читателей. Добавим к этому ещё и игнорирование проблемы множественных сравнений, когда авторы проводят попарные сравнения для трёх и большего числа сравниваемых групп. Отметим, что подобной статистической неряшливостью страдают не только начинающие аспиранты и соискатели, но и специалисты облечённые различными академическими и руководящими регалиями: академики, ректоры университетов, доктора и кандидаты наук, и многие другие учёные.

Результатом игнорирования ограничений для t-критерия Стьюдента является заблуждение авторов статей и диссертаций, а далее и читателей этих публикаций, относительно истинного соотношения генеральных средних сравниваемых групп. Так в одном случае принимается вывод о значимом различии средних, когда они на самом деле не различаются, в другом – наоборот, принимается вывод об отсутствии значимого различия средних, когда такое различие имеется.

Почему важно Нормальное распределение? Нормальное распределение важно по многим причинам. Распределение многих статистик является нормальным или может быть получено из нормальных с помощью некоторых преобразований. Рассуждая философски, можно сказать, что нормальное распределение представляет собой одну из эмпирически проверенных истин относительно общей природы действительности и его положение может рассматриваться как один из фундаментальных законов природы. Точная форма нормального распределения (характерная «колоколообразная кривая») определяется только двумя параметрами: средним и стандартным отклонением.

Характерное свойство нормального распределения состоит в том, что 68% всех его наблюдений лежат в диапазоне ± 1 стандартное отклонение от среднего, а диапазон ; ± 2 стандартных отклонения содержит 95% значений. Другими словами, при нормальном распределении, стандартизованные наблюдения, меньшие -2 или большие +2, имеют относительную частоту менее 5% (Стандартизованное наблюдение означает, что из исходного значения вычтено среднее и результат поделен на стандартное отклонение (корень из дисперсии)). Если у вас имеется доступ к пакету STATISTICA, Вы можете вычислить точные значения вероятностей, связанных с различными значениями нормального распределения, используя Вероятностный калькулятор; например, если задать z-значение (т.е. значение случайной величины, имеющей стандартное нормальное распределение) равным 4, соответствующий вероятностный уровень, вычисленный STATISTICA будет меньше .0001, поскольку при нормальном распределении практически все наблюдения (т.е. более 99,99%) попадут в диапазон ± 4 стандартных отклонения.

Графическое выражение этого распределения называется Гауссовой кривой, или кривой нормального распределения. Опытным путем установлено, что такая кривая часто повторяет форму гистограмм, получающихся при большом числе наблюдений.

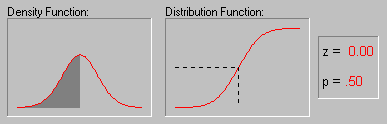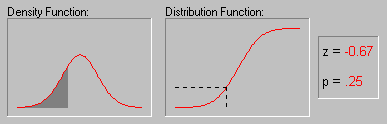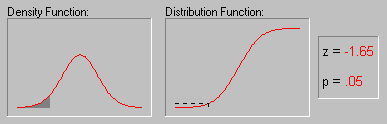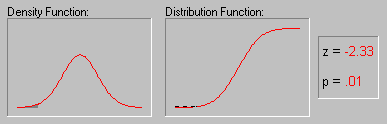
Форма кривой нормального распределения и ее положение определяются двумя величинами: генеральной средней и стандартным отклонением.

В практических исследованиях непосредственно формулой не пользуются, а прибегают к помощи таблиц.

Максимум, или центр, нормального распределения лежит в точке x = μ точка перегиба кривой находится при x1= μ - σ и x2= μ + σ , при n = ± ∞ кривая достигает нулевого значения. Размах колебаний от μ вправо и влево зависит от величины σ и укладывается в пределах трех стандартных отклонений:

1. В области пределов μ + σ находится 68,26% всех наблюдений;

2. Внутри пределов μ + 2 σ находится 95,46% всех значений случайной величины;

3. В интервале μ + 3σ находится 99,73%, практически все значения признака.

Все ли статистики критериев нормально распределены? Не все, но большинство из них либо имеют нормальное распределение, либо имеют распределение, связанное с нормальным и вычисляемое на основе нормального, такое как t, F или хи-квадрат. Обычно эти критериальные статистики требуют, чтобы анализируемые переменные сами были нормально распределены в совокупности. Многие наблюдаемые переменные действительно нормально распределены, что является еще одним аргументом в пользу того, что нормальное распределение представляет "фундаментальный закон". Проблема может возникнуть, когда пытаются применить тесты, основанные на предположении нормальности, к данным, не являющимся нормальными. В этих случаях вы можете выбрать одно из двух. Во-первых, вы можете использовать альтернативные "непараметрические" тесты (так называемые "свободно распределенные критерии", см. раздел Непараметрическая статистика и распределения). Однако это часто неудобно, потому что обычно эти критерии имеют меньшую мощность и обладают меньшей гибкостью. Как альтернативу, во многих случаях вы можете все же использовать тесты, основанные на предположении нормальности, если уверены, что объем выборки достаточно велик. Последняя возможность основана на чрезвычайно важном принципе, позволяющем понять популярность тестов, основанных на нормальности. А именно, при возрастании объема выборки, форма выборочного распределения (т.е. распределение выборочной статистики критерия , этот термин был впервые использован в работе Фишера, Fisher 1928a) приближается к нормальной, даже если распределение исследуемых переменных не является нормальным. Этот принцип иллюстрируется следующим анимационным роликом, показывающим последовательность выборочных распределений (полученных для последовательности выборок возрастающего размера: 2, 5, 10, 15 и 30), соответствующих переменным с явно выраженным отклонением от нормальности, т.е. имеющих заметную асимметричность распределения.

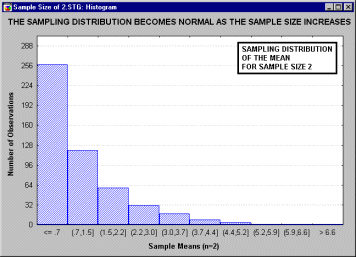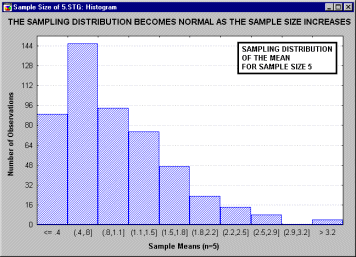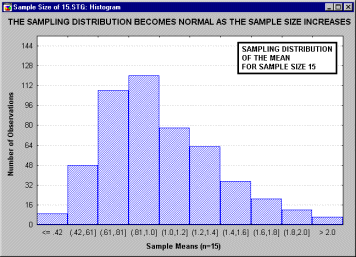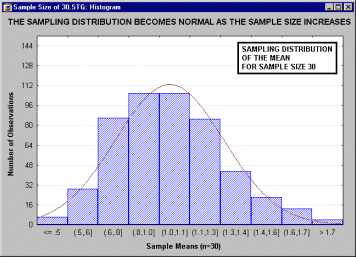
Однако по мере увеличения размера выборки, используемой для получения распределения выборочного среднего, это распределение приближается к нормальному. Отметим, что при размере выборки n=30, выборочное распределение "почти" нормально (см. на близость линии подгонки).

Статистическая надежность, или уровень вероятности – это площадь под кривой, ограниченная от среднего на t стандартных отклонений, выраженная в процентах от всей площади. Иными словами, это вероятность появления значения признака, лежащего в области μ + t σ. Уровень значимости – это вероятность того, что значение изменяющегося признака находится вне пределов μ + t σ, то есть, уровень значимости указывает вероятность отклонения случайной величины от установленных пределов варьирования. Чем больше уровень вероятности, тем меньше уровень значимости.

В практике агрономических исследований считается возможным пользоваться вероятностями 0,95 – 95% и 0,99 – 99%, которым называют доверительными, то есть такие, которым можно доверять и уверенно пользоваться. Так, при вероятности 0,95 – 95% возможность сделать ошибку 0,05 – 5%, или 1 на 20; при вероятности 0,99 – 99% - соответственно 0,01 – 1%, или 1 на 100.

Аналогичный подход применим и к распределению выборочных средних, так как всякое исследование сводится к сравнению средних величин, подчиняющихся закону нормального распределения. Средняя μ, дисперсия σ² и стандартное отклонение σ – параметры генеральной совокупности при n > ∞. Выборочные наблюдения позволяют получить оценки этих параметров. Для больших выборок (n>20-30, n>100) закономерности нормального распределения объективны для их оценок, то есть в области x ± S находится 68,26%, x ± 2S - 95,46%, x ± 3S – 99,73% всех наблюдений. Средняя арифметическая и стандартное отклонение причисляют к основным характеристикам, при помощи которых задается эмпирическое распределение измерений.

4. Методы проверки статистических гипотез

Выводы из любого сельскохозяйственного или биологического эксперимента нужно оценить с учетом их значимости, или существенности. Такую оценку проводят путем сравнения вариантов опыта друг с другом, либо с контролем (стандартом), или с теоретически ожидаемым распределением.

Статистическая гипотеза – научное предположение о тех или иных статистических законах распределения рассматриваемых случайных величин, которое может быть проверено на основе выборки. Сравнивают совокупности путем проверки нулевой гипотезы – об отсутствии реального различия между фактическими и теоретическими наблюдениями, пользуясь наиболее подходящим статистическим критерием. Если в результате проверки различия между фактическими и теоретическими показателями близки к нулю или находятся в области допустимых значений, то нулевая гипотеза не опровергается. Если же различия оказываются в критической для данного статистического критерия области, невозможны при нашей гипотезе и поэтому несовместимы с ней, нулевая гипотеза опровергается.

Принятие нулевой гипотезы означает, что данные не противоречат предположению об отсутствии различий между фактическими и теоретическими показателями. Опровержение гипотезы означает, что эмпирические данные несовместимы с нулевой гипотезой и верна другая, альтернативная гипотеза. Справедливость нулевой гипотезы проверяется вычислением статистических критериев проверки для определенного уровня значимости.

Уровень значимости характеризует, в какой мере мы рискуем ошибиться, отвергая нулевую гипотезу, т.е. какова вероятность отклонения от установленных пределов варьирования случайной величины. Поэтому, чем больше уровень вероятности, тем меньше уровень значимости.

Понятие о вероятности неразрывно связано с понятием о случайном событии. В сельскохозяйственных и биологических исследованиях вследствие присущей живым организмам изменчивости под влиянием внешних условий появление события может быть случайным либо неслучайным. Неслучайными будут такие события, которые выходят за пределы возможных случайных колебаний выборочных наблюдений. Это обстоятельство позволяет определить вероятность появления как случайных, так и неслучайных событий.

Таким образом, вероятность – мера объективной возможности события, отношение числа благопрятных случаев к общему числу случаев. Уровень значимости показывает вероятность, с которой проверяемая гипотеза может дать ошибочный результат. В практике сельскохозяйственных исследований считается возможным пользоваться вероятностями 0,95 (95%) и 0.99 (99%), которым соответствуют следующие уровни значимости 0,05 – 5% и 0,01 – 1%. Эти вероятности получили название доверительных вероятностей, т.е. таких, которым можно доверять.

Статистические критерии, используемые для оценки расхождения между статистическими совокупностями, бывают двух видов:

1) параметрические (для оценки совокупностей, имеющих нормальное распределение);

2) непараметрические (применяют к распределениям любой формы).

В практике сельскохозяйственных и биологических исследований встречаются два типа опытов.

В некоторых опытах варианты связаны друг с другом одним или несколькими условиями, контролируемыми исследователем. Вследствие этого опытные данные варьируют не независимо, а сопряженно, так как влияние условий, связывающих варианты, проявляется, как правило, однозначно. К такого типа опытам относятся, например, полевое испытание с повторностями, каждая из которых располагается на участке сравнительно одинакового плодородия. В таком опыте сопоставлять варианты друг с другом можно только в пределах повторения. Другой пример связанных наблюдений – изучение фотосинтеза; здесь объединяющим условием являются особенности каждого подопытного растения.

Наряду с этим часто сравнивают совокупности, варианты которых изменяются независимо друг от друга. Несопряженными, независимыми являются варьирование признаков растений, выращенных в разных условиях; в вегетационных опытах повторностями служат сосуды одноименных вариантов, и любой сосуд одного варианта можно сравнивать с любым сосудом другого.

Статистическая гипотеза - некоторое предположение о законе распределения случайной величины или о параметрах этого закона в рамках данной выборки.

Пример статистической гипотезы: "генеральная совокупность распределена по нормальному закону", "различие между дисперсиями двух выборок незначимо" и т.д.

Гипотеза формулируется в терминах различия величин. Например, есть случайная величина x и константа a. Они не равны (арифметически), но нужно установить, значимо ли статистически между ними различие?

Существует два типа критериев:

Необходимо отметить, что знаки ≥, ≤, = здесь используются не в арифметическом, а в «статистическом» смысле. Их необходимо читать «значимо больше», «значимо меньше», «различие незначимо».

Метод по критерию t-Стъюдента

При сравнении средних двух независимых выборок применяют метод по t – критерию Стьюдента, предложенный английским ученым Ф. Госсетом. С помощью данного метода оценивается существенность разности средних (d = x₁ – x₂). Он основан на расчете фактических и табличных значений и их сравнении.

В теории статистики ошибка разности или суммы средних арифметических независимых выборок при одинаковом числе наблюдений (n₁ + n₂) определяется по формуле:

S_d = √ S_X1² + S_X2²,

где S_d - ошибка разности или суммы;

S_X1² и S_X2² - ошибки сравниваемых средних арифметических.

Гарантией надежности вывода о существенности или несущественности различий между средними арифметическими служит отношение разницы к ее ошибке. Это отношение получило название критерия существенности разности:

t = x₁ – x₂ / "√ S_X1² + S_X2² = d / S_d.

Теоретическое значение критерия t находят по таблице, зная число степеней свободы Y = n₁ + n₂ – 2 и принятый уровень значимости.

Если t_факт ≥ t_теор , нулевая гипотеза об отсутствии существенности различий между средними опровергается, а если различия находятся в пределах случайных колебаний для принятого уровня значимости – не опровергается.

Метод интервальной оценки

Интервальная оценка характеризуется двумя числами – концами интервала, покрывающего оцениваемый параметр. Для этого следует определить доверительные интервалы для возможных значений средней генеральной совокупности. При этом, x является точечной оценкой генеральной средней, тогда точечную оценку генеральной средней можно записать так: x ± t_0,5*S_X, где t_0,5*S_X предельная ошибка выборочной средней при данном числе степеней свободы и принятом уровне значимости.

Доверительный интервал – это такой интервал, который с заданной вероятностью покрывает оцениваемый параметр. Центр интервала – выборочная оценка точки. Пределы, или доверительные границы, определяются средней ошибкой оценки и уровнем вероятности – x - t_0,5*S_X и x + t_0,5*S_X. Значение критерия Стьюдента для различных уровней значимости и числа степеней свободы приводятся в таблице.

Оценка разности средних сопряженных рядов

Оценку разности средних для сопряженных выборок вычисляют разностым методом. Сущность состоит в том, что оценивается существенность средней разности путем попарного сравнения вариантов опыта. Для нахождения S_d разностным методом вычисляют разность между сопряженными парами наблюдений d, определяют значение средней разности (d = Σ d / n) и ошибку средней разности по формуле:

S_d = √ Σ (d - d) ₂ / n (n – 1)

Критерий существенности вычисляют по формуле: t = d / S_d . Число степеней свободы находят по равенству Y= n-1, где n-1 – число сопряженных пар.

Контрольные вопросы

Контрольные вопросы

1. Что такое вариационная статистика (математическая, биологическая статистика, биометрия)?
2. Что называется совокупностью? Виды совокупностей.
3. Что называется изменчивостью, вариацией? Виды изменчивости.
4. Дайте определение вариационного ряда.
5. Назовите статистические показатели количественной изменчивости.
6. Расскажите о показателях изменчивости признака.
7. Как вычисляется дисперсия, ее свойства?
8. Какие вы знаете теоретические распределения?
9. Что такое среднее квадратическое отклонение, его свойства?
10. Какие вы знаете закономерности нормального распределения?
11. Назовите показатели качественной изменчивости и формулы их вычисления.
12. Что такое доверительный интервал и статистическая надежность?
13. Что такое абсолютная и относительная ошибка выборочной средней, как их вычислить?
14. Коэффициент вариации и его вычисление при количественной и качественной изменчивости.
15. Назовите статистические методы проверки гипотез.
16. Дайте определение статистической гипотезы.
17. Что такое нулевая и альтернативная гипотеза?
18. Что такое доверительный интервал?
19. Что такое сопряженные и независимые выборки?
20. Как вычисляется интервальная оценка параметров генеральной совокупности?