Тема №3 Взаимное положение прямой и плоскости
1. Условия принадлежности точки прямой и прямой плоскости
2. Параллельность прямой и плоскости
3. Пересечение прямой и плоскости
4. Особые прямые в плоскости
Контрольные задания по теме:
Рабочая тетрадь задача 39, задача 40а, задача 40б
1. Условия принадлежности точки прямой и прямой плоскости
Точка принадлежит прямой, если её проекции лежат на одноимённых проекциях этой прямой (рис. 21а).
Точка принадлежит плоскости, если она лежит на прямой, лежащей в этой плоскости (рис.21б).
Прямая принадлежит плоскости, если она проходит через две точки, лежащие в этой плоскости (рис.21в).
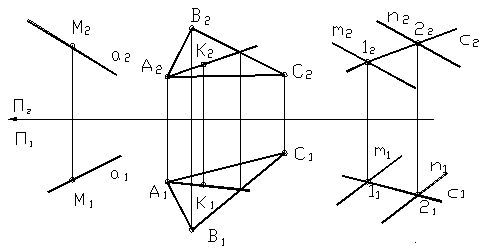
Рисунок 21
2. Параллельность прямой и плоскости
Прямая параллельна плоскости, если она параллельна любой прямой, лежащей в этой плоскости. На рисунке 22 изображена прямая t, параллельная прямой b, принадлежащей плоскости Σ: t // b Î Σ (aÇb).
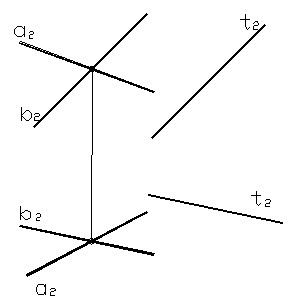
Рисунок 22
Через любую точку пространства можно провести бесконечное множество прямых, параллельных данной плоскости.
3. Пересечение прямой и плоскости
Это задача на определение общей точки прямой и плоскости. Её называют также точкой встречи. Рассмотрим пересечение прямой с плоскостью частного положения.
Плоскость Σ задана треугольником АВС и является горизонтально проецирующей плоскостью. Точка встречи прямой k с плоскостью Σ определяется по горизонтальной проекции. Фронтальная проекция точки К достраивается с помощью линии связи. Символическая запись будет выглядеть следующим образом: k ÇΣ (ABC) = K.
Видимость прямой относительно плоскости определяется при помощи фронтально-конкурирующих точек 1 и 2.
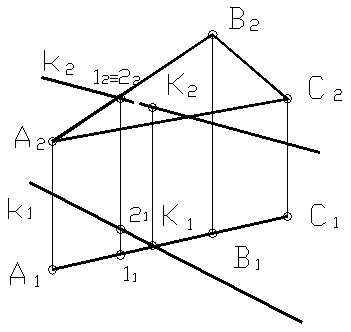
Рисунок 23
Пересечение прямой с плоскостью общего положения изображено на рисунке 24. В этом случае нужно заключить прямую в проецирующую плоскость.
t Î Σ ^ П2 – прямая t принадлежит плоскости Σ, которая перпендикулярна горизонтальной плоскости проекций. Линия пересечения этой плоскости с данной - линия (1, 2). Затем находится точка пересечения этой линии с прямой t , которая и будет являться точкой встречи прямой и плоскости. Видимость прямой относительно плоскости определяется при помощи конкурирующих точек. Возьмем горизонтально конкурирующие точки 3 и 4. Так как точка 3, принадлежащая прямой, оказалась ниже чем точка 4, следовательно, прямая на горизонтальной плоскости справа от точки пересечения невидима. Затем берем фронтально конкурирующие точки 1 и 5. Точка 1, принадлежащая плоскости, лежит ближе, следовательно, прямая находится за плоскостью, и она на фронтальной проекции невидима от точки 1 до точки К.
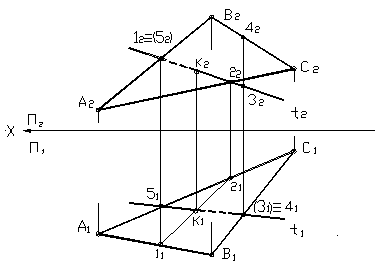
Рисунок 24
4. Особые прямые в плоскости
К особым прямым, принадлежащим плоскости, относятся горизонталь, фронталь и профильная прямая. Построение этих прямых используется при решении многих задач по начертательной геометрии. Их изображение дано на рисунке 25. Причём на горизонтальной плоскости горизонталь имеет натуральную величину, на фронтальной плоскости - фронталь и на профильной плоскости – профильная прямая.
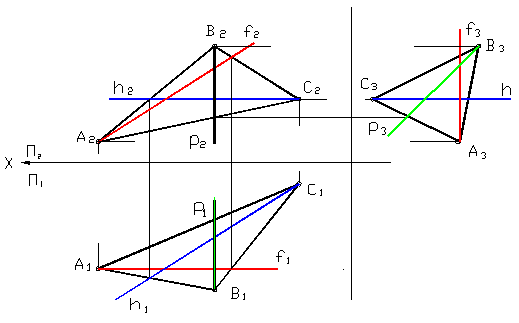
Рисунок 25
Контрольные вопросы
1. Сформулируйте условия принадлежности точки плоскости и прямой плоскости.
2. Как построить прямую параллельную заданной плоскости?
3. Вспомните этапы решения задачи на определение точки пересечения прямой и плоскости.
4. Какие точки называются конкурирующими?
5. Как провести в плоскости горизонталь и фронталь?
6. Какие еще особые прямые плоскости вы знаете?
|